【統計学】理屈を吹き飛ばして最速で答えを出すチート学問

今回は、統計学の魅力についてお話しします。

統計学は答えのないものや、個人の主観的な意見を吹き飛ばすチート学問です。

統計学を身に付けているということは、ゲームのなかでチートを使っているぐらいの破壊力があり、マリオで言うとずっとスター状態のようなものなのです。

統計は権威を吹き飛ばす！
ランダム化比較実験
1. 誤差があるものの科学的に取り扱えるようにした
2. ランダムに抽出すれば勝手に平均がとれる
理屈をもぶっとばす！統計的にそうならそう
1. 後ろ向きで短期記憶が向上するというランダム比較実験

統計は権威を吹き飛ばす！

統計学の魅力をわかっていただくために、一例を挙げてみましょう。

例えば、学生時代は従順で優等生な方が先生に好かれますよね。

しかし、ある研究では優等生よりも先生に嫌われている方がクリエイティブな傾向が高いということが言われています。

仮に学校の先生が「お前はダメだ！あの子を見習いなさい」と言おうが、統計学的に間違っているなら、この発言は間違っているのです。

そう考えると、統計学は権威をも吹き飛ばす痛快な学問なのです。

「先生、この統計によると、学校の先生から嫌われている人の方がクリエイティビティが高いと出ています。だから僕がダメな人間だという主張は根拠がないですよね？」と言えちゃうわけなのですから。(笑)

では、統計学的に合っている・間違っているの基準はなんなのでしょうか？

キーワードとなるのは、「ランダム化比較」です。

ランダム化比較実験

誤差があるものの科学的に取り扱えるようにした

ランダム化比較実験は「誤差のあるもの」を科学的に取り扱うことを可能にしました。

「誤差のないもの」とは主に自然科学の分野です。

例えば、万有引力の法則について考えてみましょう。「空中でリンゴを手放せば加速しながら地表に落下する」

こういった事象は100回試せば100回ともその通りになるものです。(りんごを空中で手放して100回やったうち99回は落ちたけど、1回は空中に止まったままでしたということは絶対にありえないと思います)

対して、「誤差のあるもの」とは主に社会科学の領域です。

例えば、心理学の世界に「フットインザドアテクニック」というものがあります。フットインザドアテクニックとは、最初にハードルの高いお願い事をすると次のお願い事が通りやすくなるというテクニックです。

例えば、まず「今からご飯に行きませんか？」という風に無理なお願いをして、あえて相手に断らせます。

次に「じゃあ明日の夜ご飯に行きませんか」という風に簡単なお願い(本命のお願い)をします。

すると、相手は最初のお願いを断った罪悪感から2番目のお願い(実は本命のお願い)を受け入れやすくなるというテクニックです。

しかし、フットインザドアテクニックは、常にうまくいくとは限りません。お願いを連続で断る人もいるでしょう。

科学的に証明するには、「普通にお願いするよりもフットインザドアテクニックでお願いする方が効果的だ」ということを証明する必要があります。

こうした証明をするために役立つのがランダム化比較実験です。

ランダムに抽出すれば勝手に平均がとれる

フットインザドアテクニックを実証するとします。

Aさんにはテクニックを使う。
Bさんには普通にお願いをする
結果、Aさんだけがお願いを受け入れてくれた。よってフットインザドアテクニックは有効である

このような実験は正しいと言えるでしょうか？答えはNoです。なぜなら、Aさんがたまたま平均よりもお人好しな人だっただけかもしれないからです。逆にBさんが平均よりも人情味の欠ける人だった可能性もあります。

そこで使えるのはランダム化です。例えば、次のようにランダムに抽出した場合はどうでしょう。

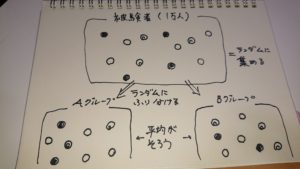
被験者として一万人の人を集めて、 5000人ずつのグループに分ける
A グループにはフットインザドアテクニックを使う
B グループには普通のお願い事を使う

ランダムに抽出した人たちを二つに分ければ双方の条件の平均はほぼ揃うようになります。

各グループの中にはものすごくお人好しな人もいるでしょうし、血も涙もない人もいるでしょう。しかし、グループ全体では大体平均値をがとれるというわけです。

ちなみに最初に集める被験者(ここでは1万人)が多ければ多いほど、平均により近くなります。ですので、規模が大きい実験ほど信頼性が高いと言えるわけです。

理屈をもぶっとばす！統計的にそうならそう

統計学は理屈さえもすっ飛ばしてしまいます。

「どうしてこんなことが起きるかよく分からないんだけど、統計的に出てるから多分そうだよ」ということが多々あるのです。

後ろ向きで短期記憶が向上するというランダム比較実験

後ろ向きで歩くことによって短期記憶が向上するという研究を見てみましょう。

被験者として114人のボランティアを集める
被験者に記憶してもらう題材として「女性が鞄を盗まれる動画を見てもらう。その後被験者を三つのグループに分ける。
①前向きに約9 M歩行してもらう
②後ろ向きに約9 M歩行してもらう
③特に何もしない
その後被験者に対して動画に関する質問を行ったところ、後ろ向きで歩行したグループが最も成績がよかった

つまり後ろ向きで歩くことによって覚えたことが記憶に定着しやすくなるということです。

なんとも不思議な現象ですが、どういう理屈があるのでしょうか。研究を率いたアレクサンダー博士は、「人間の時間認識と空間認識に相互作用があるから」という風に言っています。

これはどういうことかというと、「後ろ向きに進むということは空間的に巻き戻っているわけだから、空間認識と相互作用のある時間認識も巻き戻る。時間認識が巻き戻るということは直前に受けたテストの内容が頭の中で無意識にイメージされ、記憶に定着しやすくなる」みたいなことです。

なんともこじつけのようで納得できない理屈ですよね。理解できなくてもいいです。僕も自分で書いていてよく分かりません。(笑)

大事なのは、統計的に証明されているのなら、理屈は別に要らないというところです。実際多くの研究で、統計的にほぼ確実だけど、理由はよく分かっていないというものがあります。

例えば、「運動は脳にいい」ということはたくさんの統計学的な研究でわかっていますが、理由は定かではないようです。

「なんかよく分かんないけど統計的にそうだから」ということがあり得、それでも十分に科学的だと認められます。

さて、今回は統計学の魅力についてでした。まとめておきます。